#! https://zhuanlan.zhihu.com/p/584603600
Distortion-controlled training for E2E reverberant speech separation with aux autoencoding loss 阅读笔记
Distortion-controlled training for end-to-end reverberant speech separation with auxiliary autoencoding loss 阅读笔记
Performance of speech enhancement and separation systems in reverberant environments is yet to be explored. A core problem in reverberant speech separation is about the training and evaluation metrics. Standard time-domain metrics may introduce unexpected distortions during training and fail to properly evaluate the separation performance due to the presence of the reverberation.
We first introduce the "equal-valued contour" problem in reverberant separation where multiple outputs can lead to the same performance measured by the common metrics. We then investigate how "better" outputs with lowest target-specific distortions can be selected by auxiliary autoencoding training (A2T). A2T assumes that the separation is done by a linear operation on the mixture signal, and it adds an loss term on the autoencoding of the direct-path target signals to ensure that the distortion introduced on the direct-path signals is controlled during separation. Evaluations on separation signal quality and speech recognition accuracy show that A2T is able to control the distortion on the direct-path signals and improve the recognition accuracy.
Reverberation plays an important role in daily communications, and how to make speech enhancement and separation systems work well in reverberant environments remains a very challenging problem.
Using the reverberant clean signal as training targets introduces one core problem, equal-valued contour problem, denotes the issue that given a reference signal and a metric, there are infinite numbers of estimated signals that can achieve the same performance, which occurs in many widely-used metrics such as SNR and SI-SDR. Certain estimations among this "contour" might be more preferred than the others, however an end-to-end model may lack the ability to distinguish the "good" estimations from the "bad" ones. Just because poor results on SI-SDR doesn't mean performs not well on both WER and subjective perceptual quality measures!
Standard training configuration attempts to optimize the model to learn a linear mapping: $$ \mathcal{M}(\mathbf{x}+\sum_{i=1}^{K}\mathbf{n}_i) \approx \mathbf{x} $$
The auxiliary autoencoding term corresponds to the reconstruction of the direct-path signal of
We apply A2T in controlling the search space among the equal-valued contours in reverberant separation. We investigate ways to balance the gradients of the standard objective term and the A2T term for successful training.
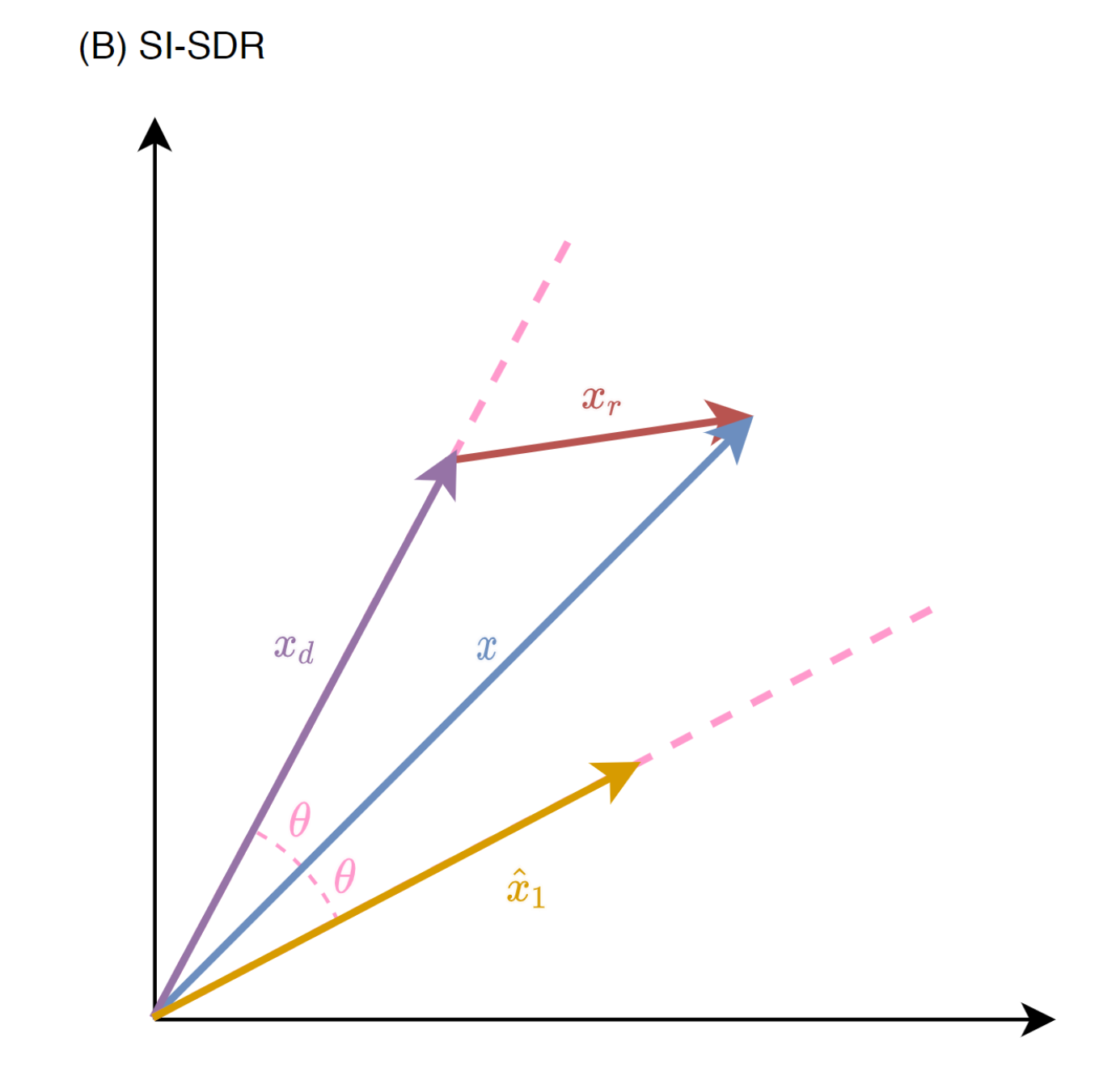
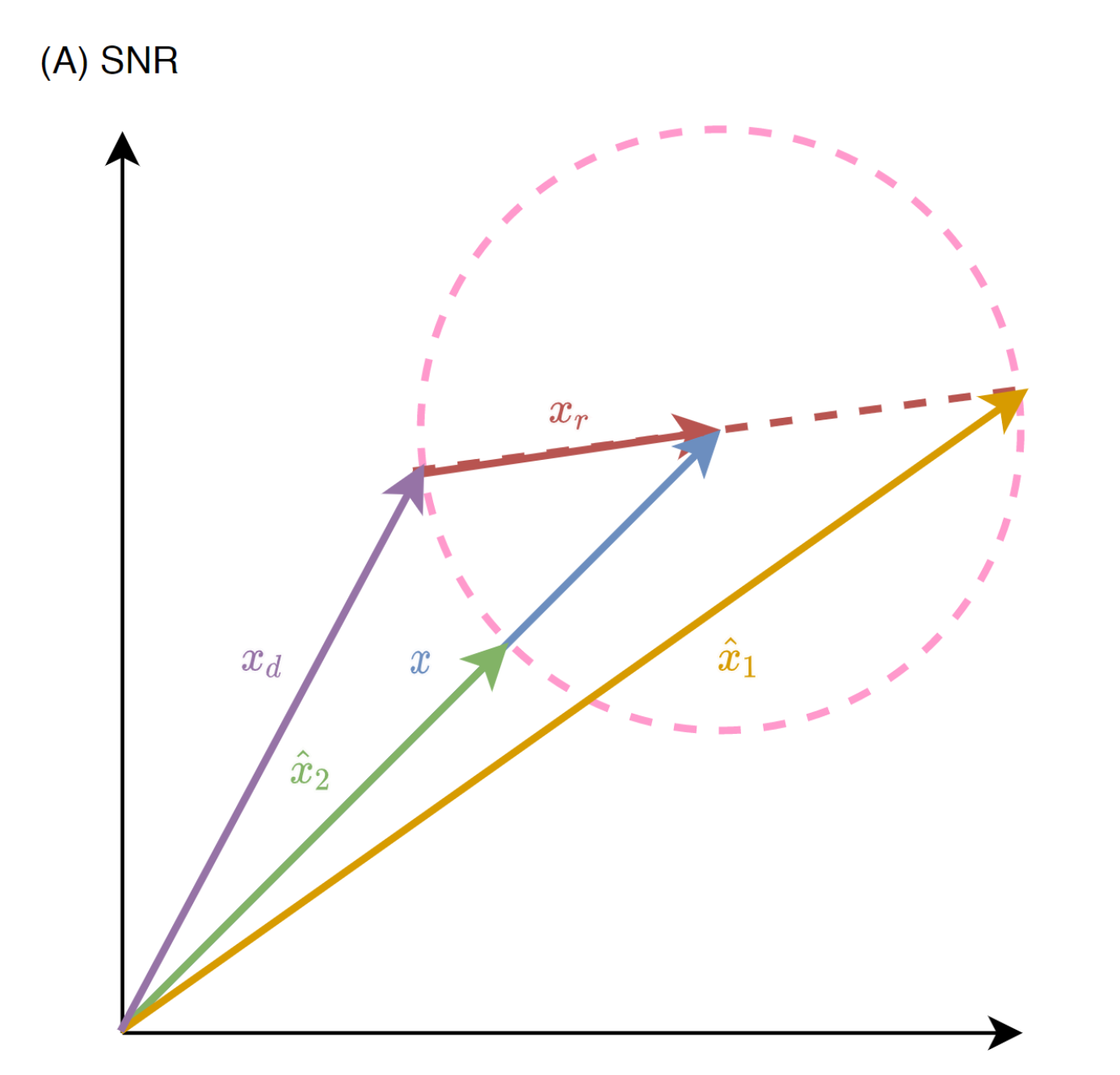 Illustration for equal-valued contours in SNR metric. The radius of the equal-valued contour is defined by the reverberation component
Illustration for equal-valued contours in SNR metric. The radius of the equal-valued contour is defined by the reverberation component
$$
\operatorname{SI-SDR}(\hat{\mathbf{x}}, \mathbf{x})=10 \log _{10}\left(\frac{c(\mathbf{x}, \hat{\mathbf{x}})^2}{1-c(\mathbf{x}, \hat{\mathbf{x}})^2}\right) \tag{9}
$$
where
Auxiliary Autoencoding Training (A2T) adds one objective term to control the system outputs on the equal-valued contours. Take
$$ \begin{aligned} \hat{\mathbf{x}}1 &=T(\mathbf{y}) \ &=T\left(\mathbf{x}^{(1)}+\sum{j=2}^C \mathbf{x}^{(j)}+\mathbf{n}\right) \ &=T\left(\mathbf{x}^{(1)}\right)+T\left(\sum_{j=2}^C \mathbf{x}^{(j)}\right)+T(\mathbf{n}) \end{aligned} \tag{10} $$
System output consists of the direct path, the late reverberation, and the interference. The conventional training objective sets the reverberant signal-of-interest
A2T adds an auxiliary autoencoding term on the direct-path signal to the objective: $$ \begin{aligned} \mathcal{L}{A 2 T} &=\underbrace{D\left(T\left(\mathbf{x}^{(1)}\right)+T\left(\sum{j=2}^C \mathbf{x}^{(j)}\right)+T(\mathbf{n}), \mathbf{x}^{(1)}\right)}_{\text {separation }} \ &+\underbrace{D\left(T\left(\mathbf{x}_d^{(1)}\right), \mathbf{x}d^{(1)}\right)}{\text {preservation }} \end{aligned} \tag{12} $$ where the auxiliary autoencoding term controls the distortion introduces to the direct-path signal and preserves its signal quality.
In the training phase, PIT is first applied on the separation term to obtain the best label permutation, and the permutation is then applied to the preservation term for auxiliary autoencoding.
Logarithm-scale objective functions such as SNR and SI-SDR are unbounded and may lead to infinitely large gradients. As autoencoding is a much easier task than separation with a much faster convergence speed, the A2T term may easily dominate the gradients and prevents the standard separation term to be in effect. [Separating Varying Numbers of Sources with Auxiliary Autoencoding Loss] proposed the
Properly adding the A2T term can almost always achieve on par or better separation performance with a significantly lower distortion on the direct-path signal. This indicates that A2T is able to find better outputs on the equal-valued contours.
The direct path room impulse response (RIR) filter in all utts is defined as the
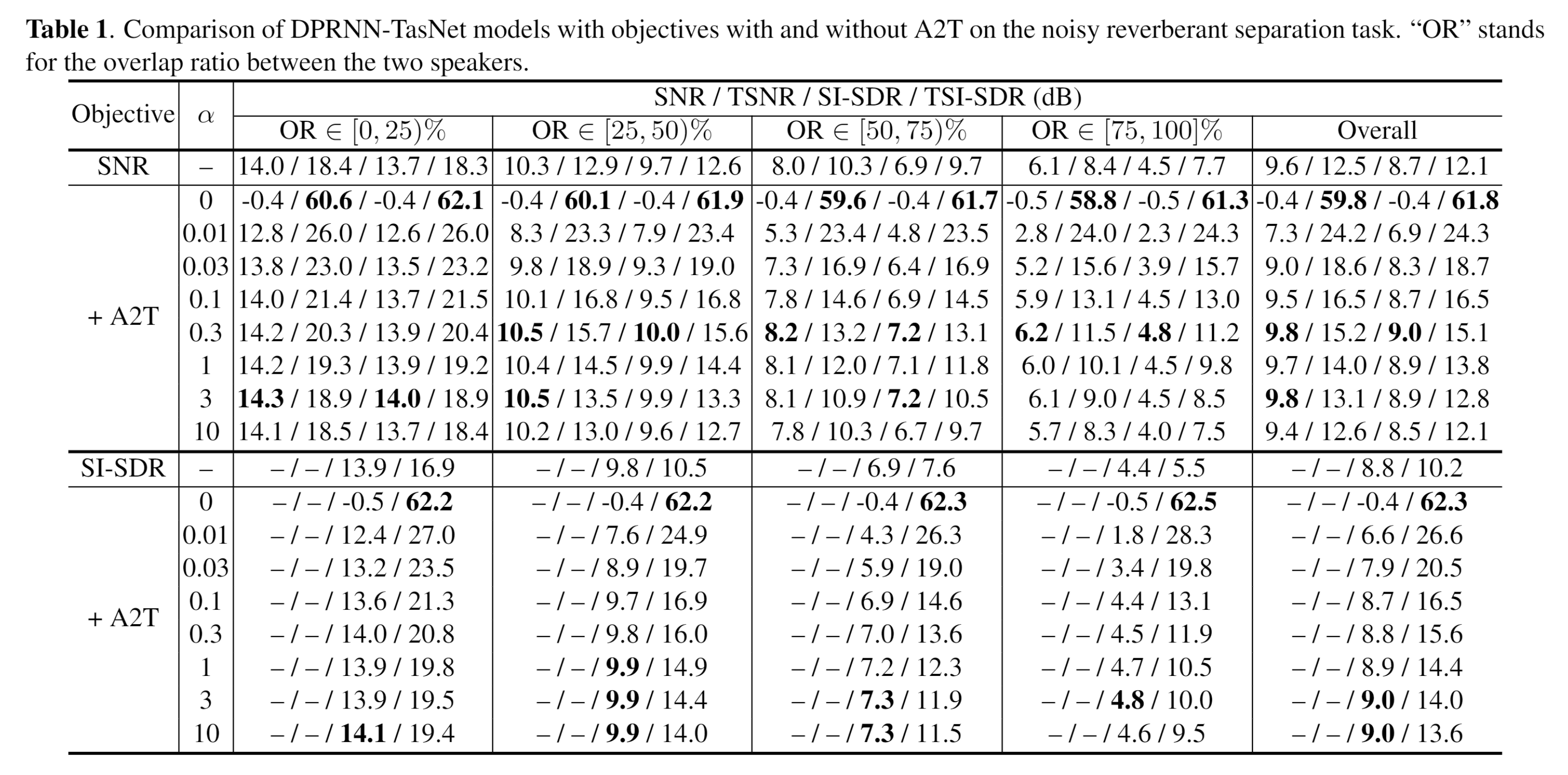 For model trained with SI-SDR, we do not report the SNR and TSNR scores as SI-SDR does not preserve the scale of the outputs.
For model trained with SI-SDR, we do not report the SNR and TSNR scores as SI-SDR does not preserve the scale of the outputs.
Moreover, SI-SDR objective even leads to a lower TSI-SDR score than the SNR objective across all overlap ratios.
Observation in Beam-TasNet and this article: SNR lead to at least on par performance as SI-SDR.
Investigated the "equal-valued contours" in commonly-used objectives and metrics for end-to-end reverberant speech separation, and proposed A2T to control the distortion introduced to the direct-path signal of the targets. A2T assumed that the separation was done by a linear operation on the mixture signal, and added an extra loss term during training to perform autoencoding on the direct-path signal of the targets.