Continuous Speech Separation with Conformer 阅读笔记.md

#! https://zhuanlan.zhihu.com/p/516114006

[语音分离] Continuous Speech Separation with Conformer 阅读笔记

Abstract

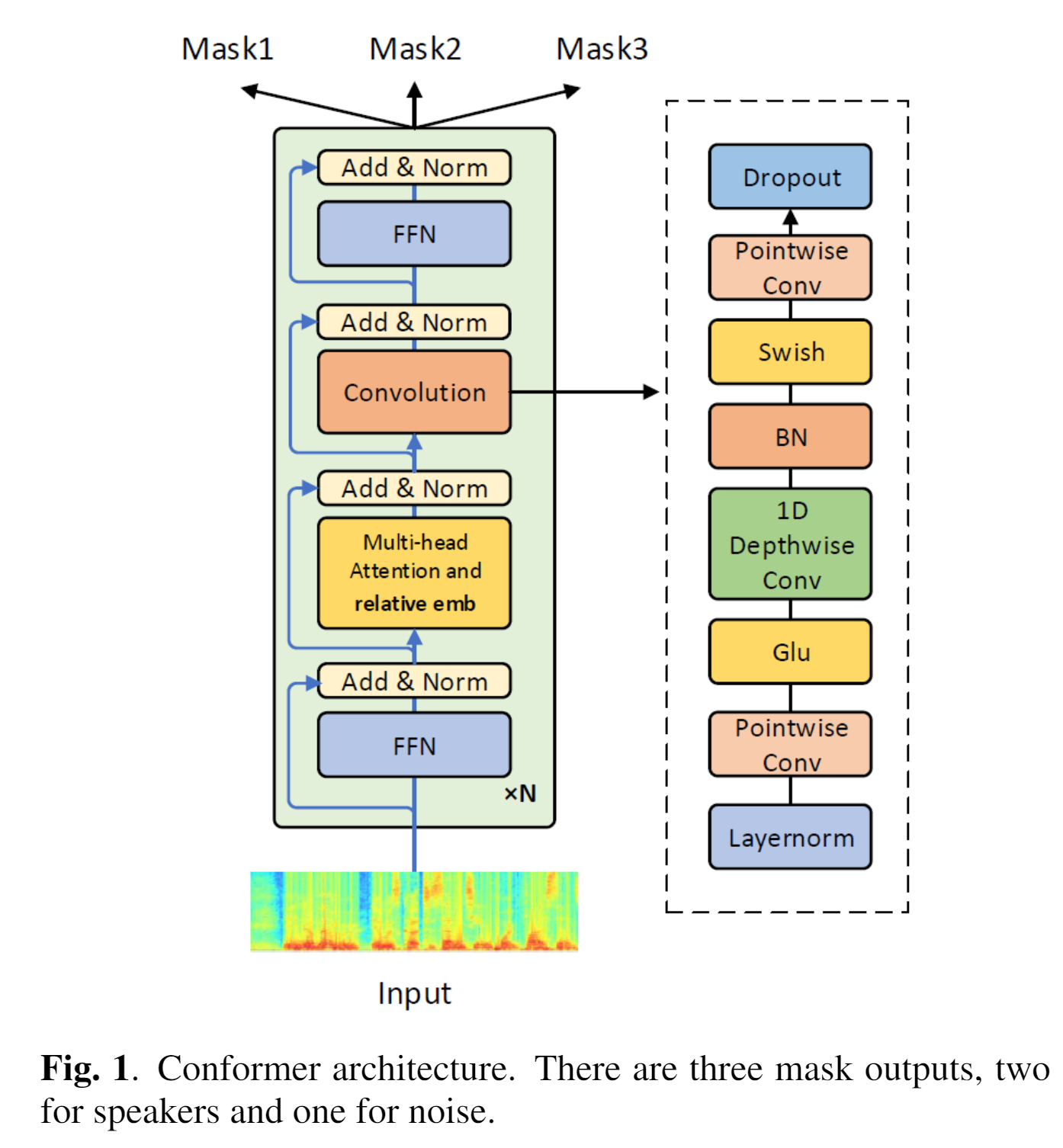
This paper examines the use of Conformer architecture in lieu of recurrent neural networks for the separation model. Conformer allows the separation model to efficiently capture both local and global context info, which is helpful for speech separation.

Introduction

When applied to acoustically and linguistically complicated scenarios such as conversation transcription, the ASR systems still suffer from the performance limitation due to overlapped speech and quick speaker turn-taking. The overlapped speech causes the so-called permutation problem.

LibriCSS (continuous speech separatoin) dataset consists of real recordings of long-form multi-talker sessions that were created by concatenating and mixing LibriSpeech utterances with various overlap ratios.

Approach

2.1. Problem Formulation

Speech separation's goal: estimate individual speaker signals from their mixture, where the source signals may be overlapped with each other wholly or partially.

$$ y(t) = \sum_{s=1}^Sx_s(t) $$ $x_s(t)$ denotes the $s$-th source signal, $y(t)$: the mixed signal. $t$ is the time index

Multi-channel setting: $$ Y(t,f) = Y^1(t,f) \oplus IPD(2)... \oplus IPD(C) $$ $\oplus$: concatenation operation

$Y^i(t,f)$: the STFT of the $i$-th channel

IPD$(i)$: the inter-channel phase difference between the $i$-th channel and the first channel [ IPD$(i)$=$\theta^i(t,f) - \theta^1(t,f)$ ]

Estimated masks ${M_s(t,f)}_{1\le s\le S}$

Estimated source STFT $X_s(t,f) = M_s(t,f) \odot Y^1(t,f)$, $\odot$ is an elementwise product.

2.2. Model structure

Each conformer block consists of a self-attention module, a convolution module, and a macron-feedforward module. A chunk of $Y(t,f)$ over time frames and frequency bins is the input of the first block. Suppose that the input to the $i$-th block is $z$, the $i$-th block output is calculated as $$ \hat{z} = z + \frac{1}{2}\text{FFN}(z)\ z^{'} = \text{selfattention}(\hat{z}) + \hat{z}\ z^{''} = \text{conv}(z^{'}) + z^{'}\ output = \text{layernorm}(z^{''} + \frac{1}{2}\text{FFN}(z^{''})) $$ In the self-attention module, $\hat{z}$ is linearly converted to $Q,K,V$ with 3 different parameter matrices. Then we apply a multi-head self-attention mechanism $$ \begin{aligned} \operatorname{Multihead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) &=\left[\mathbf{H}{\mathbf{1}} \ldots \mathbf{H}{d_{\text {head }}}\right] \mathbf{W}^{\text {head }} \ \mathbf{H}{\mathbf{i}} &=\operatorname{softmax}\left(\frac{\mathbf{Q}{\mathbf{i}}\left(\mathbf{K}{\mathbf{i}}+\mathbf{p o s}\right)^{\top}}{\sqrt{d{k}}}\right) \mathbf{V}{\mathbf{i}}, \end{aligned} $$ $d_k$ is the dimensionality of the feature vector, $d{head}$ is the number of the attention heads. $pos$ is the relative position embedding.

2.3. Chunk-wise processing for continuous separation

To deal with such long input signals, CSS generates a predefined number of signals where overlapped utterances are separated and then routed to different output channels. To enable this, we employ the chunk-wise processing proposed in [Recognizing overlapped speech in meetings: A multichannel separation approach using neural networks] at test time. A sliding-window is applied as illustrated in Fig.2, which contains 3 sub-windows, representing the history ($N_h$ frames), the current segment ($N_c$ frames), and the future context ($N_f$ frames). We move the window position forward by $N_c$ frames each time, and compute the masks for the current $N_c$ frames using the whole $N$-frame-long chunk.

Follow the LibriCSS setting for chunk-wise CSS processing, where $N_h$, $N_c$, $N_f$ are set to 1.2s, 0.8s, 0.4s respectively.

To further consider the history info beyond the current chunk, we also take account of the previous chunks in the self-attention module.

Experiment

7-channel The average overlap ratio of the training set is around 50%.

Conformer-base yielded substantial WER gains and outperformed Transformer-base, which indicates Conformer's superior local modeling capability. Larger models achieved better performance in the highly overlapped settings.

The Conformer-base obtained better WER gains for continuous input because they are good at using global info while the chunk-wise processing limits the use of context info.

Because the speech overlap happens only sporadially in real conversations, it is important for the separation model not to hurt the performance for less overlap cases.