#! https://zhuanlan.zhihu.com/p/554804094
Although the conventional mask-based MVDR (minimum variance distortionless response) could reduce the non-linear distortion, the residual noise level of the MVDR separated speech is still high.
Propose a spatio-temporal RNN based beamformer (RNN-BF) for target speech separation. This new BF framework directly learns the beamforming weights from the estimated speech and noise spatial covariance matrices. Leveraging on the temporal modeling capability of RNNs, the RNN-BF could automatically accumulate the statistics of the speech and noise covariance matrices to learn the frame-level beamforming weights in a recursive way.
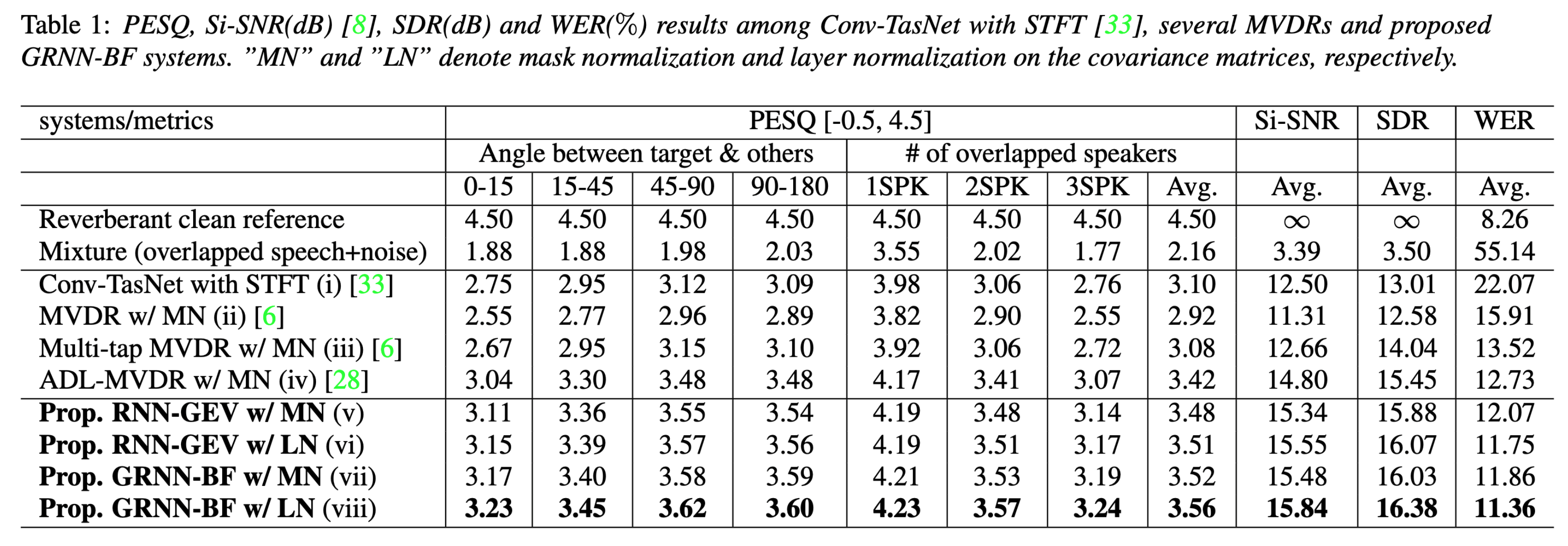
Proposed RNN-based generalized eigenvalue (RNN-GEV) beamformer and a more generalized RNN beamformer (GRNN-BF).
Mask-based MVDR achieve less non-linear distortion than "black box" NN-based speech separation methods. Most mask-based BFs are optimized in the chunk-level. The calculated beamforming weights are hence chunk-level which is not optimal for each frame.
RNN was able to solve the matrix inversion and the eigenvalue decomposition problems, which are two main matrix operations in most of the beamformers' solutions, e.g., MVDR and GEV beamformer. In the ADL-MVDR, the matrix inversion and PCA operations of traditional MVDR are replaced by two RNNs with the estimated speech and noise covariance matrices as the input.
3 contributions are made to further improve the ADL-MVDR BF.
- Propose a RNN-based GEV (RNN-GEV) BF.
- Propose a generalized RNN BF (GRNN-BF), which directly learns the frame-level BF weights from covariance matrices without following conventional beamformers' solutions.
- Replace the mask normalization with LN on the covariance matrices.
Noisy speech mixture
Clean speech
Interfering noise
In conventional mask-based BF, use a NN to predict the real valued speech mask and noise mask. Then calculate the speech / noise covariance matrix $\boldsymbol{\Phi}{\mathbf{S}}$ / $\boldsymbol{\Phi}{\mathbf{N}}$ with the predicted speech / noise mask $\mathrm{RM}{\mathbf{S}}$ / $\mathrm{RM}{\mathbf{N}}$..
$$
\boldsymbol{\Phi}{\mathbf{S}}(f)=\frac{\sum{t=1}^{T} \mathrm{RM}{\mathbf{S}}^{2}(t, f) \mathbf{Y}(t, f) \mathbf{Y}^{\mathrm{H}}(t, f)}{\sum{t=1}^{T} \mathrm{RM}{\mathbf{S}}^{2}(t, f)}
$$
where $T$ stands for the total number of frames in a chunk. The MVDR solution can be derived as,
$$
\mathbf{w}{\operatorname{MVDR}}(f)=\frac{\boldsymbol{\Phi}{\mathbf{N}}^{-1}(f) \mathbf{v}(f)}{\mathbf{v}^{\mathrm{H}}(f) \boldsymbol{\Phi}{\mathbf{N}}^{-1}(f) \mathbf{v}(f)}
\tag{3}
$$
where
GEV (generalized eigenvalue) BF:
$$
\mathbf{w}{\mathrm{GEV}}(f)=\mathcal{P}\left{\boldsymbol{\Phi}{\mathbf{N}}^{-1}(f) \boldsymbol{\Phi}_{\mathbf{S}}(f)\right}
\tag{4}
$$
The BF weights above are usually chunk-level, which is not optimal for each frame. The matrix inversion involved in Eq. (3) and Eq. (4) has the numerical instability problem.
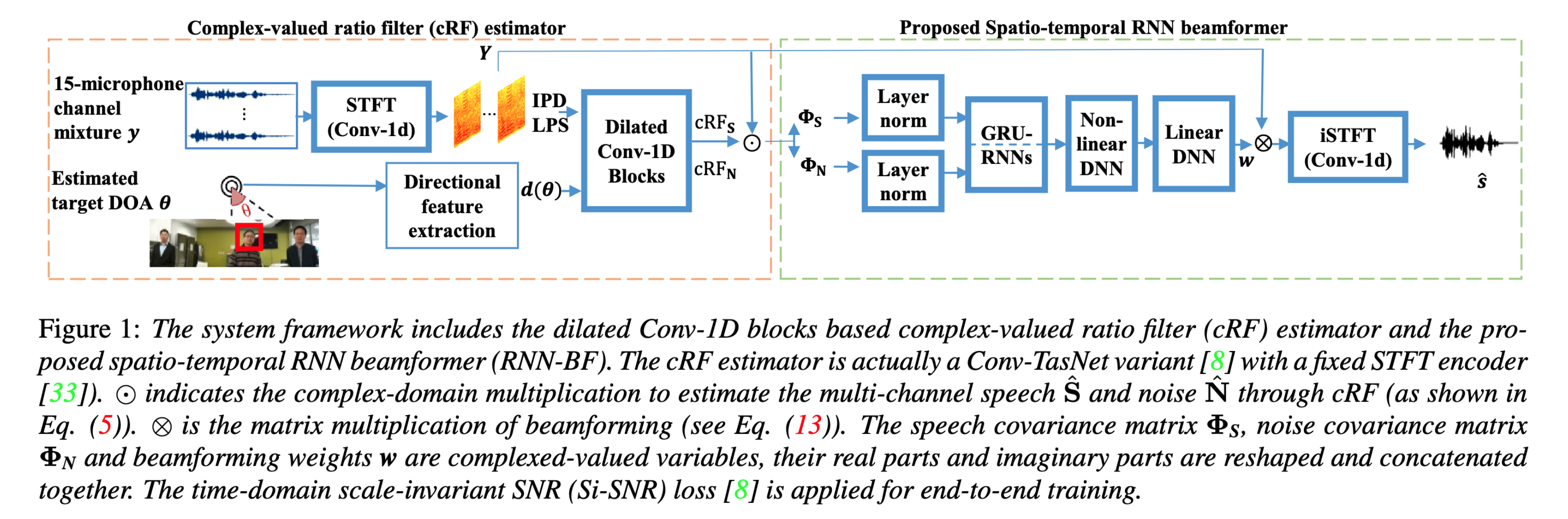 The whole system consists of a complex-valued ratio filter (cRF) estimator and the proposed spatio-temporal RNN BF. The predicted cRFs are used to calculate the covariance matrices. Then GRNN-BF learns the beamforming weights from the covariance matrices.
The whole system consists of a complex-valued ratio filter (cRF) estimator and the proposed spatio-temporal RNN BF. The predicted cRFs are used to calculate the covariance matrices. Then GRNN-BF learns the beamforming weights from the covariance matrices.
ADL-MVDR uses 2 RNNs to replace the matrix inversion and PCA in MVDR solution (defined in Eq. (3)). GRNN-BF uses RNNs to implement the GEV BF (defined in Eq. (4)). LN is proposed to replace the mask normalization, which is applied on the covariance matrices.
Firstly use cRM or cRF to estimate the speech and noise covariance matrices before using RNNs to learn the beamforming weights.
The multi-channel target speech is estimated as
$$
\hat{\mathbf{S}}(t, f)=\sum_{\tau_{1}=-K}^{\tau_{1}=K} \sum_{\tau_{2}=-K}^{\tau_{2}=K} \mathrm{cRF}{\mathbf{S}}\left(t+\tau{1}, f+\tau_{2}\right) * \mathbf{Y}\left(t+\tau_{1}, f+\tau_{2}\right)
$$
The cRF is
$\boldsymbol{\Phi}{\mathbf{S}}(t, f)$: frame-wise speech covariance matrix: $$ \boldsymbol{\Phi}{\mathrm{S}}(t, f) =\frac{\hat{\mathbf{S}}(t, f) \hat{\mathbf{S}}^{\mathrm{H}}(t, f)}{\sum_{t=1}^{T} \mathbf{cRM}{\mathrm{S}}^{\mathrm{H}}(t, f) \mathbf{cRM}{\mathrm{S}}(t, f)} $$
In this work, instead of Eq. (6), we use the LN to normalize the covariance matrices to achieve better performance. $$ \boldsymbol{\Phi}{\mathbf{S}}(t, f)=\operatorname{LayerNorm}\left(\hat{\mathbf{S}}(t, f) \hat{\mathbf{S}}^{\mathrm{H}}(t, f)\right) $$ where the LN applies per-element scale and bias with learnable affine transform, which is more flexible than the mask normalization. Another LN is adopted for $\boldsymbol{\Phi}{\mathbf{N}}(t, f)$.
Similar to ADL-MVDR, spatio-temporal RNN GEV BF also takes the estimated target speech covariance matrix $\boldsymbol{\Phi}{\mathbf{S}}(t, f)$ and the noise covariance matrix $\boldsymbol{\Phi}{\mathbf{N}}(t, f)$ as the input to predict the frame-wise BF weights.
Following the solution of the traditional GEV beamformer defined in Eq. (4), we reformulate its form in the RNN-based BF framework as
$$
\begin{aligned}
\hat{\boldsymbol{\Phi}}{\mathbf{N}}^{-1}(t, f) &=\operatorname{RNN}\left(\mathbf{\Phi}{\mathbf{N}}(t, f)\right) \
\hat{\boldsymbol{\Phi}}{\mathbf{S}}(t, f) &=\operatorname{RNN}\left(\mathbf{\Phi}{\mathbf{S}}(t, f)\right) \
\mathbf{w}{\mathbf{R N N}-\mathrm{GEV}}(t, f) &=\operatorname{DNN}\left(\hat{\boldsymbol{\Phi}}{\mathbf{N}}^{-1}(t, f) \hat{\boldsymbol{\Phi}}{\mathbf{S}}(t, f)\right) \
\hat{\mathbf{S}}(t, f) &=\left(\mathbf{w}{\mathrm{RNN}-\mathrm{GEV}}(t, f)\right)^{\mathrm{H}} \mathbf{Y}(t, f)
\end{aligned}
$$
Propose a more generalized spatio-temporal RNN BF (GRNN-BF) without following any traditional BFs' solutions.
RNN-GEV and ADL-MVDR both have 2 RNNs to deal with the target speech covariance matrix $\hat{\boldsymbol{\Phi}}{\mathbf{S}}(t, f)$ and the noise covariance matrix $\hat{\boldsymbol{\Phi}}{\mathbf{N}}(t, f)$. But GRNN-BF uses only one unified RNN-DNN to predict the frame-level BF weights directly. $$ \begin{aligned} \mathbf{w}{\mathrm{GRNN}-\mathrm{BF}}(t, f) &=\mathbf{R N N - D N N}\left(\left[\boldsymbol{\Phi}{\mathbf{N}}(t, f), \mathbf{\Phi}{\mathbf{S}}(t, f)\right]\right) \ \hat{\mathbf{S}}(t, f) &=\left(\mathbf{w}{\mathrm{GRNN}-\mathrm{BF}}(t, f)\right)^{\mathrm{H}} \mathbf{Y}(t, f) \end{aligned} $$ The input of the RNN-DNN is the concatenated tensor of $\boldsymbol{\Phi}{\mathbf{N}}(t, f)$ and $\boldsymbol{\Phi}{\mathbf{S}}(t, f)$. All of the covariance matrices and BF weights are complex-valued, we concatenate the real and imag parts of any complex-valued tensors in the whole work.
Same to ADL-MVDR
DF (DOA guided directional feature) is calculated by the cosine similarity between the target steering vector
Proposed a generalized RNN BF (GRNN-BF) that learns the frame-level beamforming weights directly from the estimated speech and noise covariance matrices. The proposed GRNN-BF with LN achieves the best objective scores.