更多细节可参照snark.js的README文件
首个使用ZK-SNARK技术的项目:Zcash,提供完全的支付保密性的去中心化网络。
其他ZKP应用:Dark Forest(第一个全链游戏);Tornado Cash(混币器):circom实现
ZK-Snark算法是零知识证明算法中的一种通用算法,可以针对任何问题高效的生成零知识协议(知识论证)。
$f$ 为关键的数学难题抽象的多项式,$λ$ 为安全变量,将$f$ 以通用逻辑不同应用拆为两部分,分别面向Prover和Verifier,
-
ZK:零知识,隐藏输入
-
Succinct:简洁性,生成可以快速验证的、简短的证明
-
Non-interactive:非交互式,不需要通过验证者和证明者反复交互来验证
通用交互式零知识证明系统如:汉密尔顿回路问题(类似七桥问题)
交互式证明可能是有缺陷的。如果一个交互式证明系统具有非零的可靠度误差(soundness error),那么一个成功的证明只能以高概率说服验证者相信其主张的真实性,而不是完全确定。与数学证明不同,数学证明在正确时会为前提和结论之间的牵连提供先验保证。(所谓先验就是不依赖于经验而获得的认识,例如在我看到人生中第一次看到圆形的东西之前,我的脑海中可能已经知道圆形是什么样子的)
Fiat-Shamir启发式(Fiat-Shamir Heurisitc):采用Hash函数的方法来把一个交互式的证明系统变成非交互式的方法。该算法允许将交互步骤中随机挑战替换为非交互随机数预言机(Random oracle)。随机数预言机即随机数函数,是一种针对任意输入得到的输出之间是相互独立切均匀分布的函数。
-
ARgument of Konwledge:知识论证,可以向验证者证明你知道输入
在零知识证明领域,1 & 2称为zk前端,3 &4称为zk后端
-
从高层次角度出发,将待解决问题转换为要隐藏输入的函数
一般为计算型问题,如图同构、离散对数等则一般有特殊设计的更为高效的方法,往往牵扯单独领域而不通过通用电路
-
将该函数转换为等效的描述电路的计算模型(R1CS/算术电路/布尔电路)
-
算术电路:一堆素数域元素中 + 和
$*$ 操作 - 简化:形式为
$x_i + x_j = x_k$ 或$x_i * x_j = x_k$ 的方程
-
算术电路:一堆素数域元素中 + 和
-
基于计算模型(如R1CS),根据不同框架的ZK System,进行算术化转换成多项式(如QAP)
可满足性问题(Boolean Satisfiability Problem),即数学难题,简称SAT问题。源于数理逻辑中经典命题逻辑关于公式的可满足性概念,是理论计算机科学中的一个重要问题,也是第一个被证明的NP-Complete问题。其表达为复杂的多项式,该多项式可以用来生成ZK-Proof。
例:
- 可满足:
$F$ =$A$ & ~$B$ ($A$ =$true$ ,$B$ =$false$ =>$F$ =$true$ ) - 不可满足:
$F$ =$A$ & ~$A$ ($F$ ==$false$ )
在 R1CS 表示中,验证者必须检查许多约束(几乎电路的每一根线都有一个约束)。二次算术程序 (Quadratic Arithmetic Program,QAP)可以 “将所有这些约束捆绑为一个电路表示”。
- 可满足:
-
利用不同 ZK System 生成 Proof。
注意不是所有的都需要承诺,比如Groth16
-
Verify
前言:证明系统分类
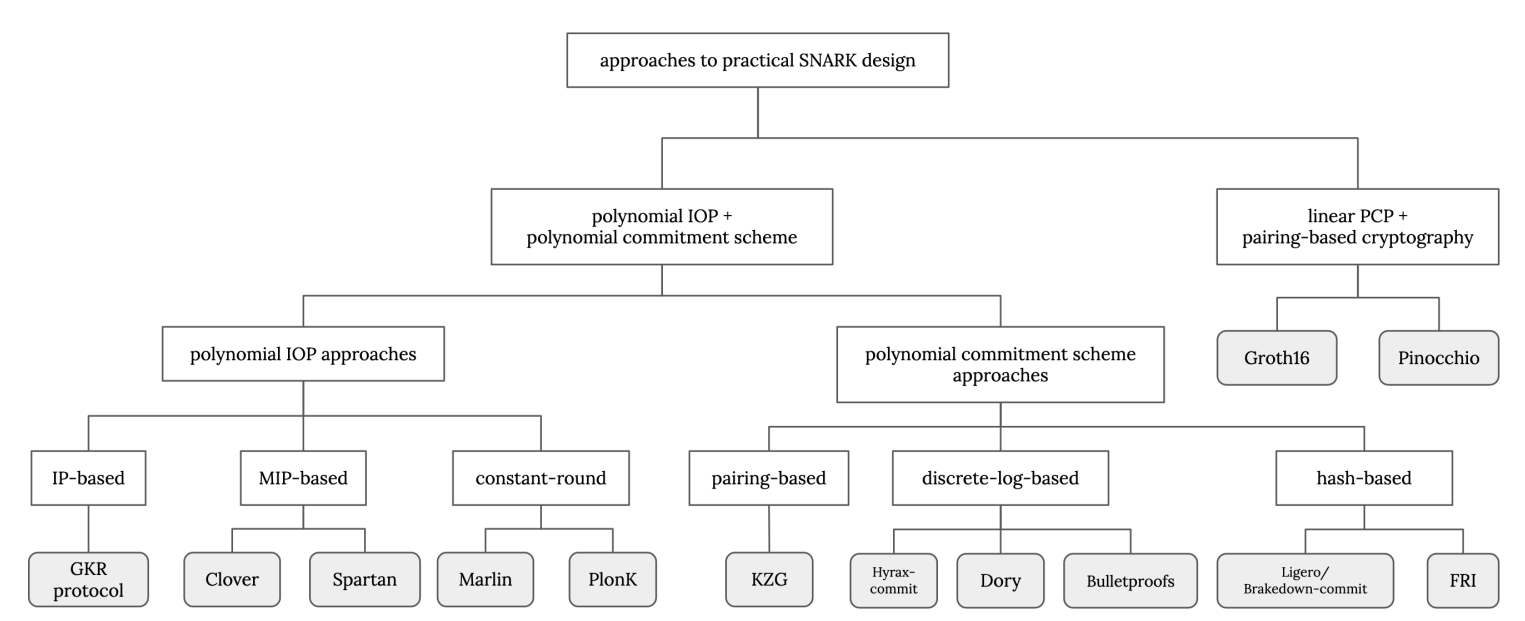
现代 SNARKs 的设计方法大多为模块化的,使用代数全息证明(Algebraic Holographic Proofs, AHPs)作为信息论组件。以下证明系统堆栈,都从 R1CS 算术化开始。不同的是,之前在 “算术化” 章节讲到的 QAP 是走linear PCP(Probabilistically Checkable Proof , PCP),Groth16正是用的该方法,其为当今热门算法之一,因为已知Groth16是目前生成证据最小的算法。
-
Polynomial IOP(Interactive Oracle Proofs):
- IP-based (交互式证明系统):证明模型,其中证明者(Prover)和验证者(Verifier)之间进行交互,以证明某个陈述的正确性。通常,这些证明可能需要多轮交互,每一轮中,验证者可能根据之前的信息提出新的问题。
- MIP-based (多重交互式证明系统):存在多个证明者,它们共同向单个验证者证明某个陈述的正确性。这些证明者可能会同时与验证者交互,但不能互相通信。通过增加证明者的数量来提高安全性和可信度。
- Constant Round:指证明的交互轮数是固定的,与证明的规模或复杂性无关。换句话说,无论要证明的陈述多么复杂,交互的轮数都保持不变。这对于实际应用非常重要,因为它保证了协议的效率,使其能够在实践中被高效地实现和使用。
-
Polynomial Commitment Scheme
Polynomial IOP 与 Polynomial Commitment Scheme区别:仅仅是交互方式的区别,即多项式 IOP (可以通过 Fiat-Shamir 变换转换成非交互式的commitment scheme)是交互式的,而多项式承诺方案通常是非交互式的。
证明者生成一个承诺,该承诺然后可以被用来生成非交互式的证明,验证者可以独立地、无需与证明者进一步交互的验证这个证明。
- 生成承诺:证明者首先对某个多项式进行承诺,这个承诺是一个加密的值,它代表了该多项式,但不透露具体的系数或者形式;
- 构建证明:证明者根据需要证明的属性(例如,某个特定点上的多项式值)构建一个证明。这个证明是基于承诺和可能的其他公共信息(例如,使用的哈希函数)生成的;
- 验证证明:验证者使用证明者提供的证明和承诺来验证多项式的某个特定属性。由于整个过程是非交互式的,验证者不需要与证明者进行任何进一步的交流。
-
线性 PCP(Probabilistically Checkable Proofs):
在不完全检查整个证明的情况下,通过随机抽样某些部分来验证证明的正确性,从而显著降低验证的复杂度。“线性”:涉及的计算和验证过程是线性的,同时也意味着证明的每个部分都与原始计算中的线性函数相关联。
通用(Universal)零知识证明发展概述:
-
阶段一:早期的古典零知识证明系统通常是为特定类型的问题量身定做的,不同应用问题的设计完全不可复用;
-
阶段二:例如 Groth16 和 Pinocchio 协议,相对于早期的零知识证明系统,提供了一种更通用的框架。可以适用于任何用算术电路表示的计算问题,确实可以被视为更universal,但他们并不是常说的universal zero knowledge protocol,因为它们都需要一个特定的受信任设置(trusted setup)阶段,这个受信任设置阶段对于每个不同的应用或电路都是唯一的,因此,针对每一个不同的电路,就需要进行一次信任设置,在这个阶段的任何点被破坏,整个系统的安全性就可能受到威胁;
-
阶段三(通用零知识证明):例如PLONK 协议就是一个通用(Universal)的零知识证明系统,尽管它确实需要一次性的受信任设置(trusted setup)。PLONK 的关键特点在于其“通用性”:一旦进行了一次受信任设置,就可以用于多种不同的计算或应用,而无需针对每个新应用重新进行设置。此外,例如 Zcash团的设计的 Halo2 协议,消除了trusted setup阶段实现了non-trusted setup的零知识证明系统。
三、例1:PLONK协议
Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge的简称,实现了Universal的零知识证明算法底层原理是多项式承诺。所谓Universal,初始可信设置(SRS)只需要一次,而且可以在原有基础上直接迭代。相比而言,Groth16的每一个电路都需要单独的可信设置(Trusted Setup)。
Plonk是属于 poly IOP (交互式Oracle证明,Interactive Oracle Proofs, IOPs) 范式,定义的多项式表达方式与Groth16不一样,属于两种并行的方式。
更多可参照 Vitalik Blog: Understanding PLONK
Plonk的基本多项式/电路表达由加法门/乘法门以及一些常量组成,下式描述的过程称为:。
- Public Input:ZeroTest
- 门约束(加法门/乘法门):ZeroTest
- 线约束 (拷贝约束):Permutation Test
门和门之间的“共享”连接,因为加法门和乘法门只描述单个门的依赖关系,所以要加上Copy约束才能描述确定的完整电路。
🌟值得一提的是,Plonk算法的关键是Plonkish的证明过程,需要引入Polynomial Commitment,通过引入不同的承诺方案Commitment可以使整个ZK系统有不同的性质,这也是相关科研论文的一个出发点,而最典型的PLONK就是使用的KZG承诺方案的。这里也可以发现,PIOP和Polynomial Commitment是相互结合使用的。
同时需要注意,证明过程中,Prover会发多个多项式给Verifier,过程是交互式的,故而归属于PIOP
-
Step1:准备工作
-
定义有限域
$𝑦^2 = 𝑥^3 + 𝑎𝑥 + b$ (椭圆曲线)做Plonk框架的第一步即选曲线:此选择域
$𝑥, 𝑦 ∈ 𝔽_{101}, 𝑎 = 0, 𝑏 = 3 => 𝑦^2 = 𝑥^3+3$ 原因:101有限域因为这个性质方便,即此处选择简单的一个举例
注意:如果是负数的话应
$Mod101$ ,根据有限域取模(集合内的元素经过加法和乘法计算,结果仍然在集合内)$100 ≡ −1$ , (理解为上溢)故推得$50 ≡ −\frac{1}{2} , 20 ≡ −\frac{1}{5}$ -
寻找
$G_1$ 循环子群生成元
$G_1=(1, 2)$ 生成元的寻找,是信息论课题研究的方向
对于原始点
$𝑃 = (𝑥, 𝑦)$ ,通过计算方法(椭圆曲线),可找到$G_1$ 子群的阶(元素的个数)为17,因为对于循环群,生成元的阶就是群的阶。-
点翻倍
计算斜率:
$𝑠 = \frac{3𝑥^2}{2𝑦}$ (对选择的曲线求导$\frac{dx}{dy}$ )假设
$2𝑃 = (𝑥, 𝑦)$ $\widehat{x} = 𝑠^2 − 2𝑥$ $\widehat{y} = 𝑠(𝑥 − \widehat{x}) − 𝑦$ 帽hat:统计学中表估计量
-
点取反
$−𝑃 = (𝑥, −𝑦)$
-
-
寻找扩展域(双线性映射)
-
寻找扩展域
$𝔽_{101^𝑘}$ ,其中$𝑘$ 是嵌入度,需要找到最小的$𝑘$ ,使得$𝑟|𝑝^𝑘 − 1$ (整除)例如 𝑘 = 2 时,
$𝑝^𝑘 − 1 = 101^2 − 1 ≡ 0(𝑚𝑜𝑑 17)$ ,即确定扩展域$𝔽_{101^2}$ -
寻找一个不可约二次式:
$𝑥^2 + 2$ $𝑢$ 为该式的解(虚数),即$𝑢^2 = −2$ ,该扩展域所有元素可写作(双线性映射方法):$𝑎 + 𝑏u$ 这里的约为有限域中概念,如
$𝑥^2$ 可以约为$x · x$ ,而$x^2+1$ 可约为$(x-100)(x+100) = x^2-100 = x^2+1$
-
-
寻找的另一循环子群
$G_2$ 计算方式同
$G_1$ ,$G_2$ 的生成元$(36, 31u)$ 计算过程复杂,可使用 sagemath 工具辅助计算
-
可信设置
-
选取安全数字
$𝑠$ ,期望只用一次,而ceremony后应该无人知晓 -
构造结构引用字符串
$SRS$ (证明者和验证者沟通时互相知晓)(两条曲线,计算方式按上述
$G_1、G_2$ 群计算法)-
$G_1$ (n+3个元素):$1 · 𝐺_1, 𝑠 ⋅ 𝐺_1, 𝑠^2 ⋅ 𝐺_1, … , 𝑠^{𝑛+2} ⋅ 𝐺_1,$ -
$G_2$ (2个元素):$1 ⋅ 𝐺_2, 𝑠 ⋅ 𝐺_2$
-
-
-
-
Step2:电路表达
-
问题电路设计
勾股数问题:
$𝛼^2 + 𝛽^2 = 𝛾^2$ 数字约束可以简化为:
-
转换为PLONK电路表达
以a = 3, b = 4, c = 5为例,a左引脚,b右引脚,c为输出,加法/乘法如有不起用则系数0
-
向量化
$𝒒_𝒍 = (0,0,0,1);𝒒_𝒓 = (0,0,0,1);𝒒_𝒐 = (−1, −1, −1 , −1) ;𝒒_𝒎 = (1 , 1 , 1 , 0) ;𝒒_𝒄 = (0 , 0 , 0 , 0)$ $𝒂 = (3 , 4 , 5 , 9); 𝒃 = (3 , 4 , 5 ,16);𝒄 = (9 ,16 ,25 ,25)$
-
转为单个多项式
利用拉格朗日插值(结果唯一):向量到多项式,如
$𝒂 = (3,4,5,9)$ 转换为坐标
$(0,3), (1,4), (2,5), (3,9)$ ,可找到穿过这些坐标的拉格朗日多项式:$\frac{1}{2}𝑥^3 − \frac{3}{2}𝑥^2 + 2𝑥 + 3 = 0$ -
拷贝约束
在之前的约束过程中,从expression到gate后,可以看到四行里每行之间没有关系。但实际上是要有一层约束,因为
$x_1 * x_1 = x_2$ ,$x_1$ 肯定要等与$x_1$ ,即比如$a_1$ 要等与$b_1$ 。
-
-
计算单位根
$H$ (定义见高等密码学运算章节)单位根在Plonk中的应用为:
$𝑛$ 需要大于等于约束向量的长度。这里长度是4,故需解出4次单位根。
原始域为
$𝔽_{101}$ ,通过循环子群的阶调整至$𝔽_{17}$ (群中元素总共17个)
即得到
-
计算陪集(coset)
陪集为子群衍生出的概念,设群
$G$ ,若$H$ 是$G$ 的一个非空子集且同时$H$ 与相同的二元运算 * 亦构成一个群,则$H$ 称为 的一个子群。在此基础上,用群$G$ 的任一元素$a$ 和子群$H$ 的任一元素运算构成的集合$aH ∈ {{a*h|h∈H}}$ 就称为陪集。(注意因为运算不一定满足交换律,故有左、右陪集之分),$aH = Ha$ 则称$H$ 关于$a$ 在$G$ 中的陪集$a_{[H]}$ ,$a$ 为代表元。$*$ 为运算省略符号陪集的性质:
- 陪集必不是子群,陪集与对应的子群没有公共元素
- 陪集中没有重复元素
- 不同的陪集没有公共元素,也就是说,利用陪集可以由子群生成一个新的子集。
PS:这里也是该原始域的优秀特性之一,很容易就找到了满足的(即元素不重叠的)
-
多项式插值法转换为多项式
注意:插值方法有很多种,这里使用多项式插值(结果不唯一)
这里,例如
$\vec{σ_1} = \vec{a} ={a_1, a_2, a_3, a_4}={2, 8, 15, 3}$ ,同理$\vec{σ_2}为 \vec{b} ,\vec{σ_3} 为 \vec{c}$ -
Step3:证明与验证(交互式)
-
证明过程(5轮)
-
承诺
$𝑎, 𝑏, 𝑐$ 得到$[a(x)]_1, [b(x)]_1, [c(x)]_1$ (编码赋值)证明者直接承诺
$[a(x)] = [a(x)]_1 = [a(x)] * G_1$ ,是个坐标 -
承诺
$𝑧$ 得到$[z(x)]_1$ (编码拷贝约束)验证者发起挑战
$acc(x)$ :累加器向量,需要从验证者得到随机数挑战$(β, γ)$ 通过插值得到累加器多项式
-
承诺
$𝑡(𝑎, 𝑏, 𝑐, 𝑧)$ 得到$t_{lo}(x) , t_{mid}(x), t_{hi}(x)$ 验证者发起挑战
$α$ 计算商多项式
$t(x)$ -
承诺
$𝑟$ 得到$\bar{a}, \bar{b}, \bar{c}, \bar{S_{σ_1}}, \bar{S_{σ_2}}, \bar{z_w}, \bar{t}, \bar{r}$ (用评估点替换$𝑡$ 内容)验证者提供评估点
计算线性化多项式
$r(x)$ -
承诺所有得到
$[W_ζ(x)]$ ,$[W_{ζw}(x)]$ 验证者提供打开挑战
$v$ 计算打开证明多项式
$W_ζ(x)$
输出证据:包括9个坐标+7个群元素,从存储和传输的角度上,坐标比群元素多占用1bit。
-
-
验证过程
-
利用
$SRS$ 预处理带入
$s$ ,先进行计算$[q_M]、[q_L]$ …… -
验证算法(11步,比较复杂,可看细节链接,此处不展开)
-
-
四、例2:Halo2 协议
基于椭圆曲线上的离散对数构建的零知识证明协议,其最大的优势是无需可信设置。即 Halo 2 不需要一个可信的初始设置过程。这意味着在生成证明系统的参数时,不需要依赖一个可信第三方来确保系统的安全性,其核心流程如图所示。
消除了“有毒废料”(toxic waste)问题:如果初始设置被破坏,整个系统的安全性可能会受到威胁。
其中,Accumulation Scheme 是通过给 accumulator(累加器)添加proofs(这些proofs是关于累加器的先前状态的),使得我们可以通过检查累加器的当前状态来检查所有先前证明是否正确(通过归纳)。