maximal-square.md

221. Maximal Square - 最大正方形

Tags - 题目标签

Description - 题目描述

EN:

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

 

Example 1:

Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] is '0' or '1'.

ZH-CN:

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

 

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

 

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

Link - 题目链接

LeetCode - LeetCode-CN

Latest Accepted Submissions - 最近一次 AC 的提交

Language	Runtime	Memory	Submission Time
typescript	4864 ms	47.4 MB	2023/03/25 18:12

function maximalSquare(matrix: string[][]): number {
  const m = matrix.length;
  const n = matrix[0].length;
  let maxArea = 0;

  const search = (x: number, y: number, width: number) => {
    if (x < 0 || x >= m) {
      return false
    }
    if (y < 0 || y >= n) {
      return false
    }

    if (width === 1) {
      return true;
    }

    if (x + width > m) {
      return false
    }

    if (y + width > n) {
      return false
    }


    if (matrix[x][y] !== '1') {
      return false;
    }


    for (let i = x; i < x + width; i++) {
      if (matrix[i][y + width - 1] !== '1') {
        return false
      }
    }

    for (let j = y; j < y + width; j++) {
      if (matrix[x + width - 1][j] !== '1') {
        return false
      }
    }

    return true;
  }

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (matrix[i][j] !== '1') {
        continue;
      }
      let width = 1;
      let ans = search(i, j, width);
      if (ans) {
        maxArea = Math.max(1, maxArea);
      }
      while (ans) {
        ans = search(i, j, width + 1);
        maxArea = Math.max(width * width, maxArea);
        width += 1;
      }
    }
  }

  return maxArea;
};

My Notes - 我的笔记

暴力法

刚开始想到的是模拟出的暴力法。 具体思想是遍历每个1，对每个1的正方形边长不断增加，增加搜索范围，当新增加的行或列不满足全为1，则返回。 想用记忆化搜索减少时间复杂度，但发现会得出错误答案，原因是不同的正方形面积会重合。 所以把这部分代码注释了：

function maximalSquare(matrix: string[][]): number {
  const m = matrix.length;
  const n = matrix[0].length;
  let maxArea = 0;
  // const mem: boolean[][] = new Array(matrix.length).fill([]).map(i => new Array(matrix.length).fill(false));

  const search = (x: number, y: number, width: number) => {
    if (x < 0 || x >= m) {
      return false
    }
    if (y < 0 || y >= n) {
      return false
    }

    if (width === 1) {
      return true;
    }

    if (x + width > m) {
      return false
    }

    if (y + width > n) {
      return false
    }


    if (matrix[x][y] !== '1') {
      return false;
    }


    for (let i = x; i < x + width; i++) {
      if (matrix[i][y + width - 1] !== '1') {
        return false
      }
    }

    for (let j = y; j < y + width; j++) {
      if (matrix[x + width - 1][j] !== '1') {
        return false
      }
    }

    // for (let i = x; i < x + width; i++) {
    //   mem[i][y + width - 1] = true;
    // }

    // for (let j = y; j < y + width; j++) {
    //   mem[x + width - 1][j] = true;
    // }

    return true;
  }

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (matrix[i][j] !== '1') {
        continue;
      }
      let width = 1;
      let ans = search(i, j, width);
      if (ans) {
        maxArea = Math.max(1, maxArea);
      }
      while (ans) {
        ans = search(i, j, width + 1);
        maxArea = Math.max(width * width, maxArea);
        width += 1;
      }
    }
  }

  return maxArea;
};

注意：边界条件和数组越界问题，以及新增的行列的下表表示，最好先画图写出式子再编码。

动态规划

参考题解：

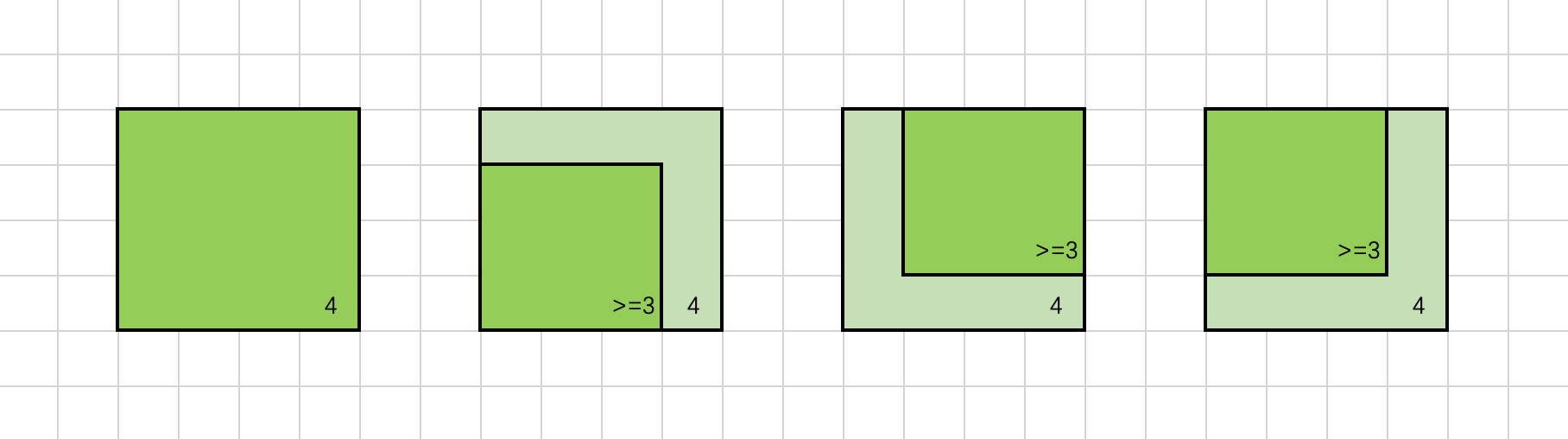
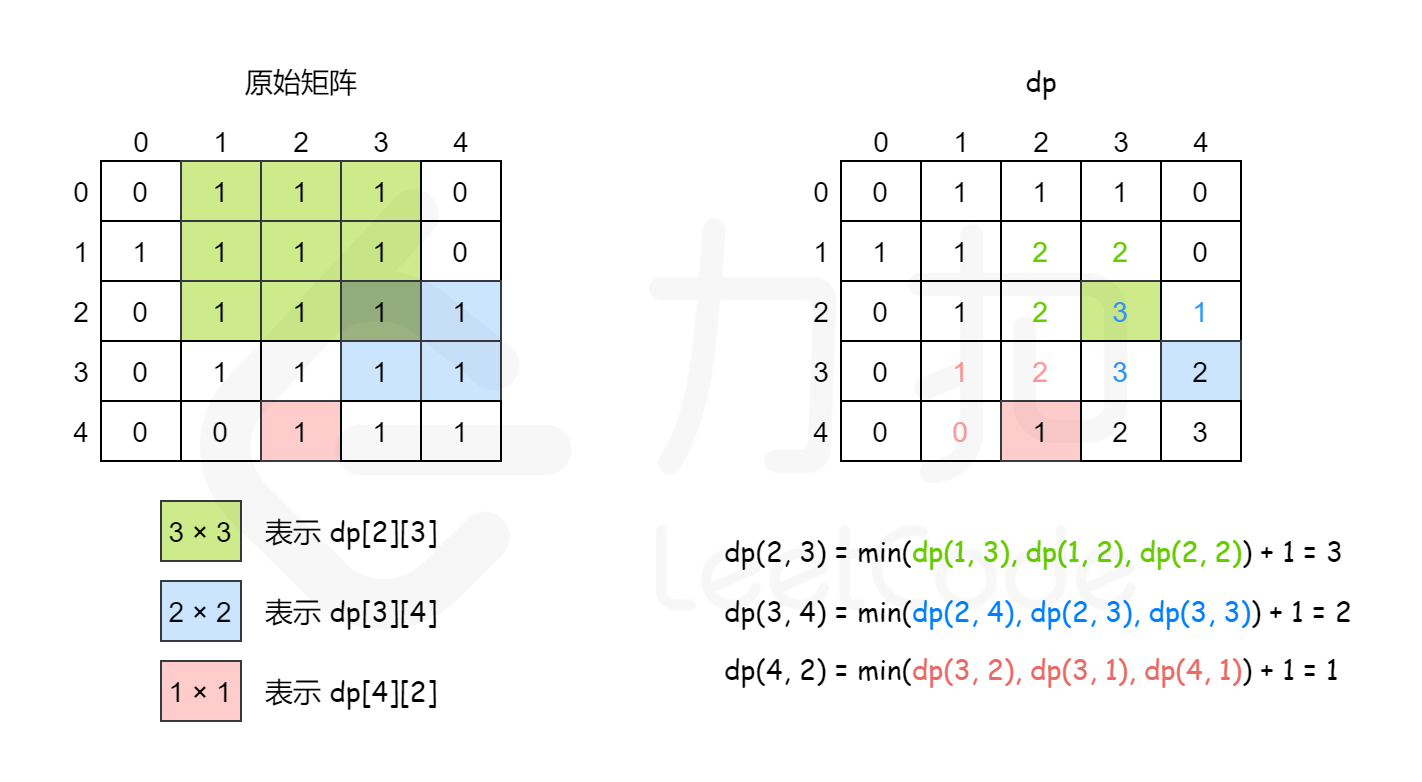
我们用 $dp(i,j)$ 表示以 $(i,j)$ 为右下角，且只包含 1 的正方形的边长最大值。如果我们能计算出所有的 $dp(i,j)$ 值，那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值，其平方即为最大正方形的面积。 $dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1$ 此外，还需要考虑边界条件。如果 iii 和 jjj 中至少有一个为 0，则以位置 $(i,j)$为右下角的最大正方形的边长只能是 1