Atestatul este live!

https://atestat-3921a.web.app/

Problema

Se da un labirint de 12 linii si n coloane (4<n<31), n este ales dinamic. Sa se gaseasca cel mai scurt drum din coltul STANGA SUS pana la coltul din DREAPTA JOS al labirintului. Traversand labirintul nu avem voie sa folosim elementele de tip wall.

Rezolvare

Am folosit algoritmul Dijkstra si A* pentru rezolvarea propriu-zisa a problemei din punct de vedere algoritmic. Vizual, elemente de CSS si Javascript vor fi folosite pentru a ilustra nodurille verificate in timp real si la final cel mai scurt drum dintre cele doua puncte alese.

Elemente folosite pentru realizarea proiectului

• Algoritmi si structuri de date
  • Cautarea informata
  • Dijkstra si A*
  • Coada prioritara
  • Functii euristice
  • Matricea
  • Vectorul de aparitii
• Limbaje de programare, estetica, hosting si version control
  • Javascript ES6
  • HTML & CSS
  • Firebase
  • Git
  • Node Package Manager (NPM)
• Librarii folosite
  • React JS
  • Firebase Github Actions
  • NPM
• Notiuni folosite pentru implementarea proiectului
  • Programare functionala (React Hooks, algoritmii de cautare)
  • Programare Obiect-Orientata (Componentele React)
  • Programare ASYNC-ronista (update la starea cautarii automata fara nevoia unui refresh)
  • Optimizarea algoritmilor prin folosirea tehnicii de informare
  • Hosting folosind o baza de date NoSQL (Firebase)

Scopul proiectului si ideea

Motivul pentru care am ales aceasta tema este interesul meu in algormiti optimi si pentru a vedea in timp real diferenta dintre un algoritm de cautare informat si unul normal. Lucrurile care se pot gasii pe interent despre aceste algorimuri aplicate pe grafuri sunt vaste si interesante, avand aplicatii in viata de zi cu zi cum ar fi Apple si Google Maps. Cu totii stim despre faimosul algoritm Dijkstra care gaseste cea mai scurta distanta dintre doua puncte ale unui graf prin folosirea unei structuri de date abstracte si anume ,,Cozii de prioritati''. Un videoclip care explica foarte bine acest algoritm este cel de la Computerphile, linkul este aici. Am incercat atunci si eu sa explic intr-un mod vizual cum se cauta cel mai scurt drum dintre doua puncte intr-un graf.

Acest proiect reuseste sa ilustreze intr-un mod interactiv gasirea celui mai scurt drum intre 2 puncte ale unui graf cu mentionaria faptului ca graful nostru este o matrice de 12 linii cu coloane generate dinamic de utilizator (intre 5 si 30) fiind prezente si noduri la care nu avem access sub forma unor ziduri. Nodurile sunt elemente ale matricii, iar costul traversarii intre nodurile vecine este de valoare egala(1). Am vizualizat gasirea celui mai scurt drum prin aplicarea algoritmului Dijkstra si al unui alt algoritm mai elegant si optim ca acesta, A*.

Cum folosim vizualizatorul?

Alegerea algoritmului este a utilizatorului inainte de a genera labirintul se va selecta 0 pentru A* sau 1 pentru Dijkstra dupa care se va apasa butonul Submit. Doar dupa aceea putem genera labirintul alegand numarul de coloane si apasand dupa butonul GENEREAZA. Vizualizarea va incepe dupa apasarea butonului Vizualizeaza si daca doriti as introduceti date noi apasati mai intai butonul Refresh.

Daca generearea initiala nu functioneaza continuati sa incercati, acest lucru este datorat modului de implementare ales, nu vor fi acceptate labirinte in care nu exista o legatura directa intre cele 2 puncte astfel programul da refresh paginii web

---

Ce este algoritmul A*?

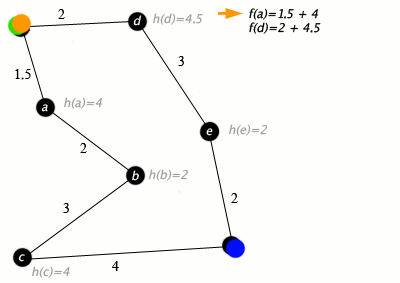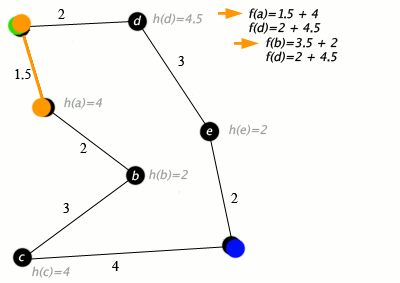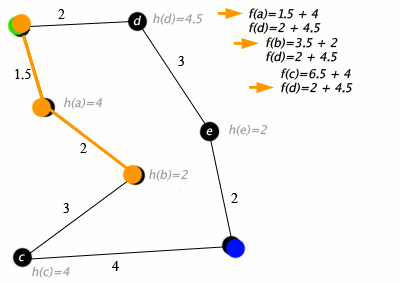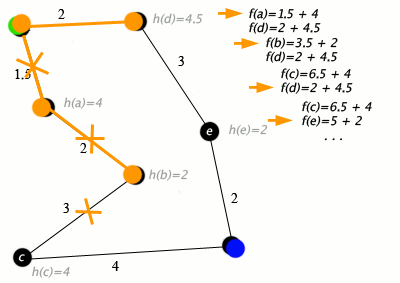
A * este un algoritm de parcurgere a graficului si cautare de cai, care este adesea utilizat în multe domenii ale informaticii datorita completitudinii, optimitatii si eficientei sale. Dupa cum am spus deci A* este un Dijkstra mai optim, in videoclipul de mai jos observam cum functioneaza algoritmul.

Algoritmul nu verifica in intregime partea stanga a grafului, lucru care Dijkstra l-ar fi facut, deoarece se indeparteaza de punctul final. Daca acesta nu gaseste cel mai scurt drum indreptandu-se spre partea punctul final acesta se va calcula si probabilitatea de a se indeparta de nodul final, doar pe urma. A* incearca a urmarii destinatia finala si deci sa isi gaseasca calea prin labirint folosindu-se de faptul ca stie unde este punctul de final si coordonatele punctului care il analizeaza. Pentru ca acest lucru sa fie indeplinit in spatiul 2D al matricei generate se foloseste de o functie euristica ,,Manhattan distance''. Aceasta este data de functia prezenta in fisierul astar.js:

function heuristic(a, b){
    let d = Math.abs(a.x-b.x) + Math.abs(a.y - b.y)
    return d
}

Aceasta este apelata la fiecare calcul al valorii unui nod din graf vecin celui care este in calcul in prezent, fiecare nod din graf va fi suma valorii de distanta normala parcursa (G) si distanta euristica (H) formand funcita (F) definita mai jos:

// Analiza valorilor f,h si g al unui nod vecin celui curent

neighbour.h = heuristic(neighbour, endNode);
neighbour.g = current.g + 1
neighbour.f = neighbour.h + neighbour.g;


// current este nodul pe care ne aflam
// neigbour este nodul care il calculam, fiind pozitionati pe nodul current

Dupa ce a calculat valoarea f aceasta va fi comparata la intrarea in coada de prioritati pe o pozitie relativa cu valoarea f (se incearca verificarea nodurilor cu o valoare f cat mai mica). Procesul se repeta pentru toti vecinii nodului curent, dupa ce toti au fost adaugati in coada cu prioritati se trece la urmatorul nod iar cel mai scrut traseu este mereu pastrat in memorie. Algoritmul se va oprii cand ne aflam la nodul de final si va creea un vector path care contine cel mai scurt drum care trebuie urmat prin ,,backtracking'' intorcandu-se la valoarea sa initiala:

if (current === endNode){
    let temp = current;
    path.push(temp);
    while (temp.prev){
       path.push(temp.prev);
       temp = temp.prev;
    }
    return {path, visitedNodes}
}

In cazul in care nu s-a ajuns la un nod final if-ul de mai sus este ignorat iar algoritmul isi continua procesul de a analiza toti vecinii nodului curent astfel:

// selectam vecinii
var neighbours = current.neighbours;

for (let i=0; i<neighbours.length; i++){
    let neighbour = neighbours[i];
    // daca nodul care il analizam nu este un perete si nu este deja analizat continuam
    if (!closedSet.includes(neighbour) && !neighbour.isWall){
        let tempG = current.g + 1; // g-ul creste
        let newPath = false;
        // se verifica daca nodul curent este deja in nodurile candidate pentru a fi cel mai scurt drum
        if (openSet.includes(neighbour)){
            if (tempG < neighbour.g){
                neighbour.g = tempG;
                newPath = true;
            } 
        } else {
            neighbour.g = tempG;
            newPath = true; 
            openSet.push(neighbour);
        }
        
        if (newPath){
            // calculam valoarea finala f in functie de algoritmul ales
            // Dijkstra are f=g iar A* are f=h+g
            if (choice == 0){
                neighbour.h = heuristic(neighbour, endNode);
            } else {
                neighbour.h = 0
            }
            neighbour.f = neighbour.h + neighbour.g;
            neighbour.prev = current;
        }
    }
}

Dupa executarea acestui for vom merge din nou in programul principal care nu se va oprii cat timp exista inca noduri candidate sau am gasit un drum la nodul final. Se va executa o cautare a nodului cu cea mai mica valoare f astfel:

let leastIndex = 0;
for (let i=0; i<openSet.length; i++){
    if (openSet[i].f < openSet[leastIndex].f){
        leastIndex = i;
    }
}

---

Demonstratie a aplicatiei