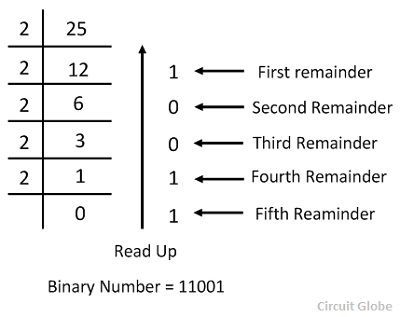
For converting to base 2, we can use the double dabble method.
Observation: Value of every even power of -2 will be same as that of even power of 2, eg. (-2)^4 = (2)^4. Hence, every alternate bit in base 2 representation of a number would become negative, i.e. for (7) base 10 => (0111) base 2 => (-1) * 0*(2^3) + 1*(2^2) + (-1) * 1*(2^1) + 1*(2^0) => (3) base 10
Intuition: Using the double dabble method, we can obtain exactly half the bits right for base -2 representation. It must mean we have to adjust the rule for calculating odd-powered bits. After some trial and error, I could obtain the correct base -2 representation by performing double dabble for base 2, except now while dividing the number at every alternate step, I ceiled the integer instead of flooring.
| Divisor | Dividend | Remainder |
|---|---|---|
| 2 | 7 | 1 |
| 2 | 3 (floor 7/2 ) | 1 |
| 2 | 2 (ceil 3/2 ) | 0 |
| 2 | 1 (floor 2/2) | 1 |
| 2 | 1 (ceil 1/2 ) | 1 |
| 2 | 0 (floor 1/2 ) | 0 |
https://leetcode.com/problems/convert-to-base-2/discuss/265868/1ms-runtime-with-explanation