Skip to content

Latest commit

 

History

History
140 lines (128 loc) · 4.12 KB

1568. Minimum Number of Days to Disconnect Island.md

File metadata and controls

140 lines (128 loc) · 4.12 KB

1568. Minimum Number of Days to Disconnect Island

the third one in Weekly Contest 204.

Difficulty : Medium

Related Topics : Greedy

Given a 2D grid consisting of 1s (land) and 0s (water). An island is a maximal 4-directionally (horizontal or vertical) connected group of 1s.

The grid is said to be connected if we have exactly one island, otherwise is said disconnected.

In one day, we are allowed to change any single land cell (1) into a water cell (0).

Return the minimum number of days to disconnect the grid.

Example 1:

1

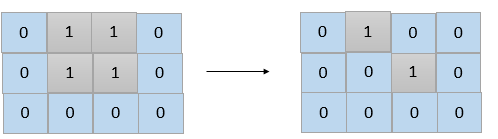
Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
Output: 2
Explanation: We need at least 2 days to get a disconnected grid.
Change land grid[1][1] and grid[0][2] to water and get 2 disconnected island.

Example 2:

Input: grid = [[1,1]]
Output: 2
Explanation: Grid of full water is also disconnected ([[1,1]] -> [[0,0]]), 0 islands.

Example 3:

Input: grid = [[1,0,1,0]]
Output: 0

Example 4:

Input: grid = [[1,1,0,1,1],
               [1,1,1,1,1],
               [1,1,0,1,1],
               [1,1,0,1,1]]
Output: 1

Example 5:

Input: grid = [[1,1,0,1,1],
               [1,1,1,1,1],
               [1,1,0,1,1],
               [1,1,1,1,1]]
Output: 2

Constraints:

  • 1 <= grid.length, grid[i].length <= 30
  • grid[i][j] is 0 or 1.

Solution

  • mine
    • Java
      • Runtime: 25 ms, faster than 90.72%, Memory Usage: 39 MB, less than 87.28% of Java online submissions 
        //O(R^2 * C^2)time
//O(R^2 * C^2)space
public int minDays(int[][] grid) {
    int r = grid.length;
    int c = grid[0].length;
    boolean[][] used = new boolean[r][c];
    int count = 0, size = 0;
    for (int i = 0; i < r; i++) {
        for (int j = 0; j < c; j++) {
            if (grid[i][j] == 0) continue;
            size++; //size the vaule 1
            //get the max island
            count = Math.max(count, dfs(grid, used, i, j));
        }
    }
    // if size of vaule 1 is not equal count  , so it is disconntected reutrn 0.
    if (size != count) return 0;
    //if just one vaule 1, return 1
    if (size == 1) return 1;

    // check if remove one value 1,  if can made it is disconntected return 1;  otherwise return 2.
    for (int i = 0; i < r; i++) {
        for (int j = 0; j < c; j++) {
            if (grid[i][j] == 0) continue;
            grid[i][j] = 0;
            int res = 0;
            boolean[][] t = new boolean[r][c];
            if (i > 0 && grid[i - 1][j] == 1) {
                res = dfs(grid, t, i - 1, j);
            } else if (i + 1 < grid.length && grid[i + 1][j] == 1) {
                res = dfs(grid, t, i + 1, j);
            } else if (j > 0 && grid[i][j - 1] == 1) {
                res = dfs(grid, t, i, j - 1);
            } else if (j + 1 < grid[i].length && grid[i][j + 1] == 1) {
                res = dfs(grid, t, i, j + 1);
            }
            if (res + 1 != size) return 1;
            grid[i][j] = 1;
        }
    }
    return 2;
}

int dfs(int[][] grid, boolean[][] used, int i, int j) {
    if (used[i][j]) return 0;
    int res = grid[i][j];
    used[i][j] = true;
    if (i > 0 && grid[i - 1][j] == 1) {
        res += dfs(grid, used, i - 1, j);
    }
    if (i + 1 < grid.length && grid[i + 1][j] == 1) {
        res += dfs(grid, used, i + 1, j);
    }
    if (j > 0 && grid[i][j - 1] == 1) {
        res += dfs(grid, used, i, j - 1);
    }
    if (j + 1 < grid[i].length && grid[i][j + 1] == 1) {
        res += dfs(grid, used, i, j + 1);
    }
    return res;
}