the last one in Weekly Contest 208.
Difficulty : Hard
Related Topics : Dynamic Programming
We have
nbuildings numbered from0ton - 1. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.You are given an array
requestswhererequests[i] = [fromi, toi]represents an employee's request to transfer from buildingfromito buildingtoi.All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if
n = 3and two employees are leaving building0, one is leaving building1, and one is leaving building2, there should be two employees moving to building0, one employee moving to building1, and one employee moving to building2.Return the maximum number of achievable requests.
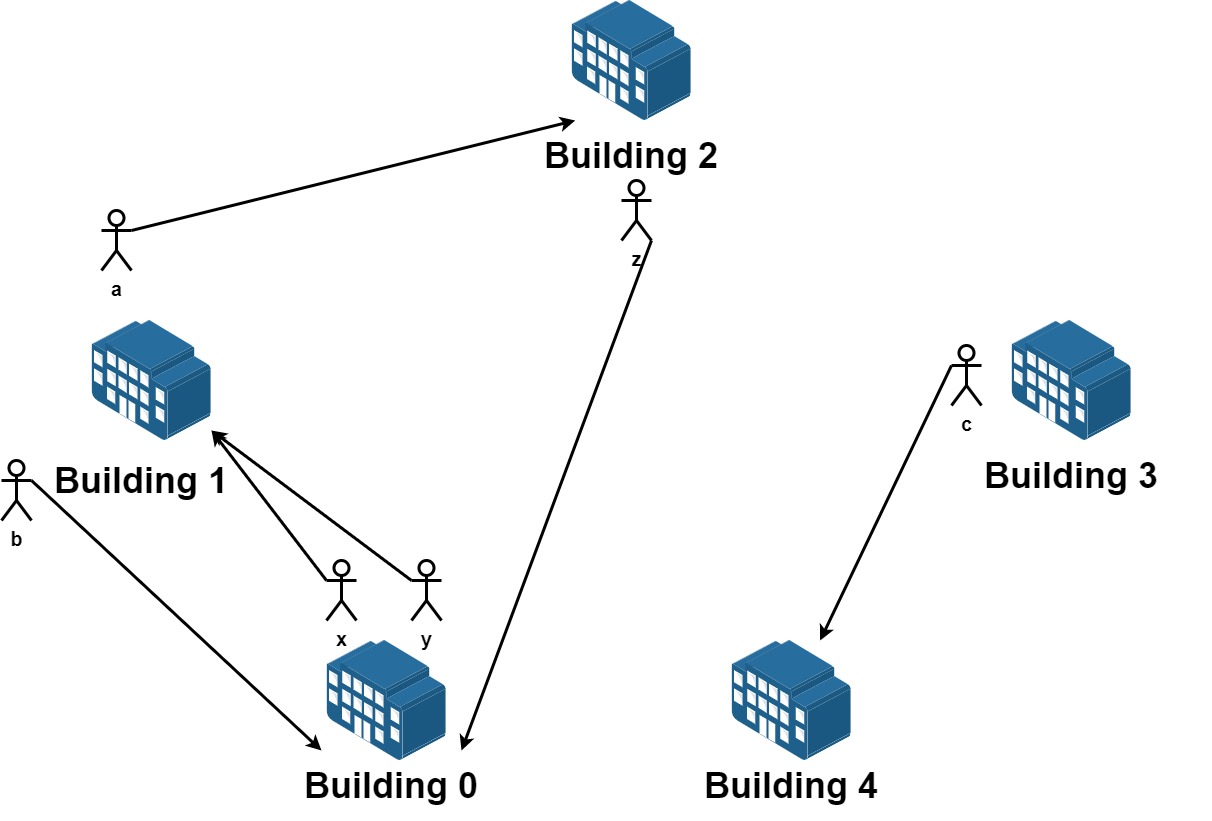
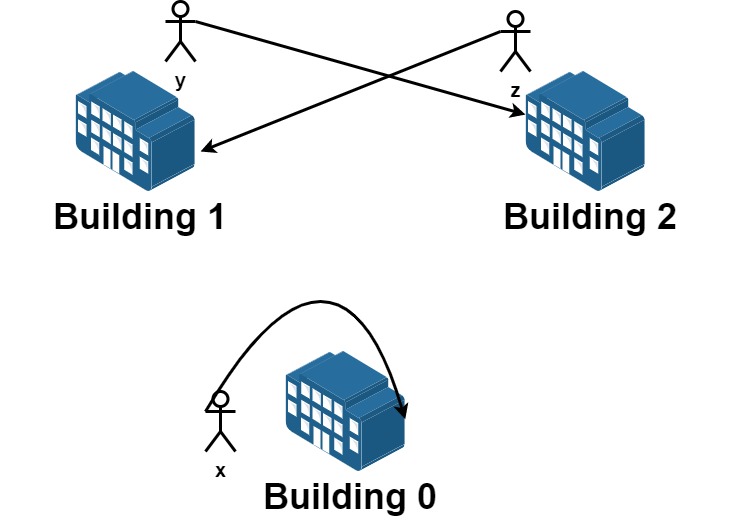
Input: n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]] Output: 5 Explantion: Let's see the requests: From building 0 we have employees x and y and both want to move to building 1. From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively. From building 2 we have employee z and they want to move to building 0. From building 3 we have employee c and they want to move to building 4. From building 4 we don't have any requests. We can achieve the requests of users x and b by swapping their places. We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.Input: n = 3, requests = [[0,0],[1,2],[2,1]] Output: 3 Explantion: Let's see the requests: From building 0 we have employee x and they want to stay in the same building 0. From building 1 we have employee y and they want to move to building 2. From building 2 we have employee z and they want to move to building 1. We can achieve all the requests.Input: n = 4, requests = [[0,3],[3,1],[1,2],[2,0]] Output: 4
1 <= n <= 201 <= requests.length <= 16requests[i].length == 20 <= fromi, toi < n
- mine
- Java
- got from the discuss
Runtime: 26 ms, faster than 71.76%, Memory Usage: 36.6 MB, less than 8.46% of Java online submissions// O(2^N)time // O(N)space // n = requests.length int res = 0; public int maximumRequests(int n, int[][] requests) { check(requests, 0, new int[n], 0); return res; } void check(int[][] r, int index, int[] arr, int changed) { if (index == r.length) { for (int i : arr) { if (i != 0) return; } res = Math.max(res, changed); return; } //change index arr[r[index][0]]--; arr[r[index][1]]++; check(r, index + 1, arr, changed + 1); //not change index arr[r[index][0]]++; arr[r[index][1]]--; check(r, index + 1, arr, changed); }
- got from the discuss
- Java
- the most votes
Runtime: 26 ms, faster than 71.76%, Memory Usage: 36.6 MB, less than 8.46% of Java online submissionsint max = 0; public int maximumRequests(int n, int[][] requests) { helper(requests, 0, new int[n], 0); return max; } private void helper(int[][] requests, int index, int[] count, int num) { // Traverse all n buildings to see if they are all 0. (means balanced) if (index == requests.length) { for (int i : count) { if (0 != i) { return; } } max = Math.max(max, num); return; } // Choose this request count[requests[index][0]]++; count[requests[index][1]]--; helper(requests, index + 1, count, num + 1); count[requests[index][0]]--; count[requests[index][1]]++; // Not Choose the request helper(requests, index + 1, count, num); }
- the fastest code
Runtime: 1 ms, faster than 100.00%, Memory Usage: 36.6 MB, less than 8.46% of Java online submissionsint[][] map; public int maximumRequests(int n, int[][] requests) { map = new int[n][n]; int res = 0; int len = requests.length; for (int i = 0; i < len; i++) { int from = requests[i][0]; int to = requests[i][1]; if (from == to) { res++; continue; } map[from][to]++; } return res + maxReHelper(0, n); } private int maxReStartFromMinNodeHelper(int minNode, int len) { int result = 0; for (int i = minNode + 1; i < len; i++) { if (map[minNode][i] > 0) { map[minNode][i]--; int res = dfsHelper(minNode, i, 1, len); result = Math.max(res, result); map[minNode][i]++; } } return result; } private int maxReHelper(int minNode, int len) { int result = 0; for (int i = minNode; i < len; i++) { result = Math.max(maxReStartFromMinNodeHelper(i, len), result); } return result; } private int dfsHelper(int start, int lastNode, int steps, int len) { if (lastNode == start) { return steps + maxReHelper(start, len); } int result = 0; for (int i = start; i < len; i++) { if (map[lastNode][i] > 0) { map[lastNode][i]--; int res = dfsHelper(start, i, steps + 1, len); result = Math.max(res, result); map[lastNode][i]++; } } return result; }