the last one in Weekly Contest 207.
Difficulty : Hard
Related Topics : Dynamic Programming、Graph
You are given two groups of points where the first group has
size1points, the second group hassize2points, andsize1 >= size2.The
costof the connection between any two points are given in ansize1 x size2matrix wherecost[i][j]is the cost of connecting pointiof the first group and pointjof the second group. The groups are connected if each point in both groups is connected to one or more points in the opposite group. In other words, each point in the first group must be connected to at least one point in the second group, and each point in the second group must be connected to at least one point in the first group.Return the minimum cost it takes to connect the two groups.
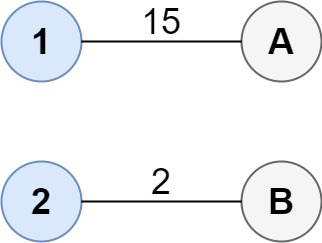
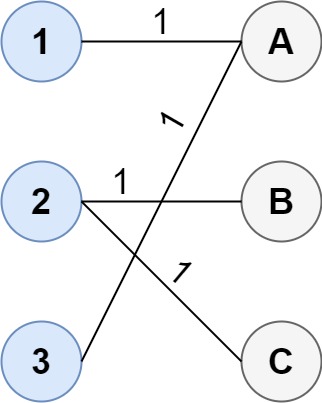
Input: cost = [[15, 96], [36, 2]] Output: 17 Explanation: The optimal way of connecting the groups is: 1--A 2--B This results in a total cost of 17.Input: cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]] Output: 4 Explanation: The optimal way of connecting the groups is: 1--A 2--B 2--C 3--A This results in a total cost of 4. Note that there are multiple points connected to point 2 in the first group and point A in the second group. This does not matter as there is no limit to the number of points that can be connected. We only care about the minimum total cost.Input: cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]] Output: 10
size1 == cost.lengthsize2 == cost[i].length1 <= size1, size2 <= 12size1 >= size20 <= cost[i][j] <= 100
- mine
- Java
- ``
- ``
- Java
- the most votes
- DP
Runtime: 12 ms, faster than 100.00%, Memory Usage: 38.6 MB, less than 94.96% of Java online submissions// O((n * 2^m) * m)time // O(N * 2^m)space public int connectTwoGroups(List<List<Integer>> cost) { int l = cost.size(), r = cost.get(0).size(); int[] right = new int[r]; Arrays.fill(right, Integer.MAX_VALUE); for (int j = 0; j < r; j++) { for (int i = 0; i < l; i++) { right[j] = Math.min(right[j], cost.get(i).get(j)); } } return helper(cost, 0, right, 0, new int[l + 1][(1<<r)]); } private int helper(List<List<Integer>> cost, int i, int[] right, int mask, int[][] dp) { if (dp[i][mask] > 0) return dp[i][mask]; int len = right.length; int res = 0; if (i < cost.size()) { res = Integer.MAX_VALUE; for (int j = 0; j < len; j++) { res = Math.min(res, cost.get(i).get(j) + helper(cost, i + 1, right, mask | (1 << j), dp)); } } else { for (int j = 0; j < len; j++) { if ((mask & (1 << j)) == 0) res += right[j]; } } return dp[i][mask] = res; }
- the fastest code
- DFS & Memorize
Runtime: 7 ms, faster than 100.00%, Memory Usage: 38.5 MB, less than 93.41% of Java online submissions// O((n * 2^m) * m)time // O(n * 2^m)space public int connectTwoGroups(List<List<Integer>> mat) { final int N = mat.size(); final int M = mat.get(0).size(); int[][] cost = toCostArray(mat); int[] cheapDict = getCheapDict(cost); Integer[][] memo = new Integer[N + 1][1 << M]; return dfs(memo, cost, cheapDict, 0, 0, N, M); } private int dfs(Integer[][] memo, int[][] cost, int[] cheapDict, int curr, int mask, final int N, final int M) { if (memo[curr][mask] != null) { return memo[curr][mask]; } if (curr >= N) { int minCost = 0; for (int j = 0; j < M; ++j) { if ((mask & (1 << j)) == 0) { minCost += cheapDict[j]; } } memo[curr][mask] = minCost; } else { int minCost = Integer.MAX_VALUE; for (int j = 0; j < M; ++j) { minCost = Math.min(minCost, cost[curr][j] + dfs(memo, cost, cheapDict, curr + 1, mask | (1 << j), N, M)); } memo[curr][mask] = minCost; } return memo[curr][mask]; } private int[] getCheapDict(int[][] cost) { final int N = cost.length; final int M = cost[0].length; int[] cheapDict = new int[M]; for (int j = 0; j < M; ++j) { cheapDict[j] = Integer.MAX_VALUE; for (int i = 0; i < N; ++i) { cheapDict[j] = Math.min(cheapDict[j], cost[i][j]); } } return cheapDict; } private int[][] toCostArray(List<List<Integer>> mat) { final int N = mat.size(); final int M = mat.get(0).size(); int[][] cost = new int[N][M]; for (int i = 0; i < N; ++i) { for (int j = 0; j < M; ++j) { cost[i][j] = mat.get(i).get(j); } } return cost; }