Skip to content

Latest commit

 

History

History
106 lines (92 loc) · 3.39 KB

240. Search a 2D Matrix II.md

File metadata and controls

106 lines (92 loc) · 3.39 KB

240. Search a 2D Matrix II

leetcode Daily Challenge on Febrary 23th, 2021.

Difficulty : Medium

Related Topics : BinarySearch、Divide and Conquer

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

  • Integers in each row are sorted in ascending from left to right.
  • Integers in each column are sorted in ascending from top to bottom.

Example 1:

1

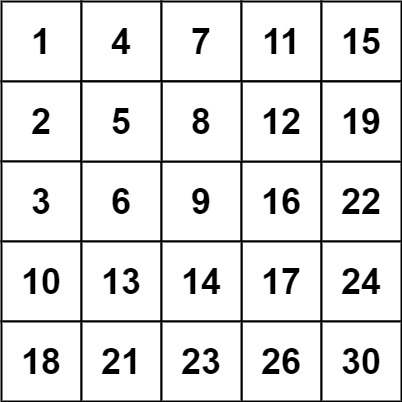
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

2

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -10^9 <= matix[i][j] <= 10^9
  • All the integers in each row are sorted in ascending order.
  • All the integers in each column are sorted in ascending order.
  • -10^9 <= target <= 10^9

Solution

  • mine
    • Java
      • BinarySearch && Divide and Conquer Runtime: 7 ms, faster than 35.94%, Memory Usage: 44.5 MB, less than 80.88% of Java online submissions 
        public boolean searchMatrix(int[][] matrix, int target) {
    final int m = matrix.length;
    if (m == 0 || matrix[0].length == 0) {
        return false;
    }
    final int n = matrix[0].length;

    return searchMatrix(matrix, target, 0, m - 1, 0, n - 1);
}

public boolean searchMatrix(int[][] matrix, int target, int rowStart, int rowEnd, int colStart, int colEnd) {
    int rowMiddle = rowStart + (rowEnd - rowStart) / 2;
    int colMiddle = colStart + (colEnd - colStart) / 2;
    if (rowStart > rowEnd || colStart > colEnd) {
        return false;
    }
    int valMiddle = matrix[rowMiddle][colMiddle];
    if (target == valMiddle) {
        return true;
    }
    if (target < valMiddle) {
        return searchMatrix(matrix, target, rowStart, rowEnd, colStart, colMiddle - 1)
                || searchMatrix(matrix, target, rowStart, rowMiddle - 1, colMiddle, colEnd);
    } else {
        return searchMatrix(matrix, target, rowStart, rowEnd, colMiddle + 1, colEnd)
                || searchMatrix(matrix, target, rowMiddle + 1, rowEnd, colStart, colMiddle);
    }
}
  • the most votes
  • Runtime: 4 ms, faster than 100.00%, Memory Usage: 45.1 MB, less than 22.36% of Java online submissions 
    public boolean searchMatrix(int[][] matrix, int target) {
    if(matrix == null || matrix.length < 1 || matrix[0].length <1) {
        return false;
    }
    int col = matrix[0].length-1;
    int row = 0;
    while(col >= 0 && row <= matrix.length-1) {
        if(target == matrix[row][col]) {
            return true;
        } else if(target < matrix[row][col]) {
            col--;
        } else if(target > matrix[row][col]) {
            row++;
        }
    }
    return false;
}